ما هي معضلة عيد الميلاد؟

عندما نفكر في كل الأيام التي يمكن أن نحتفل فيها بعيد ميلاد – بما في ذلك يوم 29 فبراير ، والذي يأتي مرة واحدة كل 4 سنوات – سيكون هناك 366 يومًا محتملاً لميلادك. إذا قابلت شخصًا ما في الشارع ، فما هو احتمال أن يكون لديك نفس عيد الميلاد (اليوم والشهر ، وليس السنة)؟
ليس احتمال حقيقي ، أليس كذلك؟ لذلك إذا صادفتك شخصًا يشاركك نفس عيد ميلادك ، فإن أول ما يتبادر إلى ذهنك هو مدى ندرة هذه المصادفة.
أذن، كم عدد الأشخاص الذين تحتاجهم في غرفة واحدة لضمان فرصة بنسبة 50٪ على الأقل أن يكون لشخصين نفس عيد الميلاد؟

ربما تعتقد أنه يجب عليك تجمع 183 شخصًا – نصف العدد البالغ 366 – على الأقل احصل على هذا. لكن، هل تعتقد أنك تحتاج فقط إلى إضافة 23 شخصًا للحصول على فرصة بنسبة 50٪ لوجود شخصين في نفس عيد الميلاد؟ هل هذا يبدو مستحيلا؟
ربما ، لكن هذا صحيح! هذه مشكلة حسابية تسمى مشكلة عيد الميلاد.
بالتأكيد إنها ليست معضلة منطقية تمامًا – لأنه لا يمكن التراجع عنها – لكنها غريبة جدًا لدرجة أنها تسمى معضلة عيد الميلاد – أو التناقض.
لن ندخل في التعقيدات الرياضية ونفترض أن هناك 365 عيد ميلاد محتملاً لأي واحد منا. إذا دخلت غرفة بها 22 شخصًا ، فإن أول ما يتبادر إلى الذهن هو احتمال العثور على شخص له نفس تاريخ ميلادك هو 365 – 22 = 343.
لننظر إلى الأمر بطريقة أخرى: بدلاً من مقارنة أعياد ميلاد بعضنا البعض ، فلنقارن أعياد ميلاد بعضنا البعض بالأخرى في الغرفة (بدلاً من 365 يومًا في السنة).
وفقًا لذلك ، يقارن الأول يومه بـ 22 يومًا آخر ، والثاني بـ 21 يومًا آخر ، والثالث بـ 20 يومًا ، وهكذا. إذا جمعنا كل هذه المقارنات (22 + 21 + 20 + … + 1) ، فسنحصل على 253 زوجًا من الاحتمالات (توجد معادلة رياضية لهذا) ، وكلما زادت احتمالية إيجاد اثنين متطابقين.
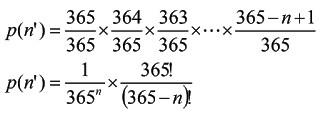 |
كما اتفقنا ، لن تدخل في التعقيدات الرياضية ، لكن احتمال عيد ميلاد الشخص الأول هو 365/365 ، والثاني 364/365 ، وهكذا ، إذا وصلنا إلى الشخص الثالث والعشرين ، فإن احتماله هو 343 / 365. رياضيا ، إذا ضربنا كل الاحتمالات الناتجة الثلاثة والعشرين ، نحصل على الاحتمال = 0.491
وفي قوانين الاحتمال 1 – 0.491 = 0.509 ، هذا يعني أن هناك فرصة بنسبة 50.9٪ لوجود شخصين من بين 32 شخصًا في نفس التاريخ.